

Rimoyt.com
Темы: машиностроение, САПР, 3d моделирование, техническое образование, промышленные предприятия, технические вузы

Начертательная геометрия - раздел геометрии, в котором пространственные фигуры (цилиндр, конус, пирамида), которые состоят из точек, линий, поверхностей изучаются по их проекциям на плоскости (или другой поверхности).
Основные задачи, которые включает рабочая программа курса - создание метода изображения геометрических фигур на плоскости/поверхности (то есть из 3D в 2D) и разработка способов решения позиционных и метрических задач.
Начертательная геометрия развивает пространственное воображения, что очень важно для инженера, особенно инженера-конструктора, который в будущем будет выполнять чертежи и 3D модели.
Начертательную геометрию обычно проходят во втором семестре первого курса, выполняют по ней графические работы и заполняют рабочую тетрадь, в конце семестра сдают экзамен. Предмет считается очень сложным, особенно, если проходить его в течение всего одного семестра. После начертательной геометрии (геометрическое черчение, проекционное черчение) студенты проходят инженерную графику (машиностроительное черчение).
Основные разделы и понятия
Раздел
| Ключевые слова |
|---|---|
| Метод проекций | Центральное проецирование Параллельное проецирование Ортогональное проецирование |
| Способы преобразования ортогональных проекций |
Способ плоскопараллельного перемещения Способ замены плоскостей проекций |
| Линия | Пространственные кривые линии Плоские кривые линии |
| Поверхность | Нелинейчатые поверхности Линейчатые поверхности Поверхности параллельного переноса, вращения |
| Позиционные задачи | Принадлежность точки поверхности Определение точек пересечения линии с поверхностью Построение линий пересечения двух поверхностей |
| Метрические задачи | Определение расстояния между точками, прямыми, плоскостями Определение углов между прямой и плоскостью, плоскостями, скрещивающимися прямыми |
| Развертка поверхностей | Развертка поверхности многогранников Развертка развертывающихся поверхностей |
| Аксонометрические проекции | Диметрическая проекция Изометрическая проекция |
Графические работы
 |
Общие правила оформления Обычно - задание оформить титульный лист. В процессе выполнения этого задания по начертательной геометрии студент знакомится с необходимыми ГОСТами - 2.301-68 Форматы, 2.303-68 Линии, 2.304-81 Шрифты чертёжные - в соответствии с которыми он и оформляет титульный лист к своему альбому чертежей. |
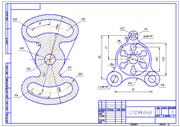 |
Геометрическое черчение Для построения чертежей деталей необходимо выполнить ряд геометрических построений (способ решения задачи чертежными инструментами). Задание часто дают по темам Сопряжение (плавный переход от одной линии к другой) и Конусность (уклон одной прямой к другой и конусность усеченного конуса можно определить также по формулам). |
 |
Проекционное черчение. Аксонометрические проекции Упражнение 1. По двум заданным видам построить третий. Выполнить фронтальный (или горизонтальный) разрезы, построить изображение детали в прямоугольной аксонометрии Упражнение 2. По двум заданным видам построить третий. Выполнить фронтальный, профильный разрезы и наклонное сечение. В первых двух упражнениях должны быть использованы разные аксонометрические проекции: пряомугольная изометрия и прямоугольная диметрия. Упражнение 3. По двум заданным видам построить третий, выполнить необходимые разеры, построить линии пересечения и перехода. Упражнение 4. Построить два заданных вида, выполнить необходимые разрезы. Построить линии среза. Данное задание, как и некоторые другие, может присутствовать в курсе по инженерной графике, а не начертательной геометрии. |
 |
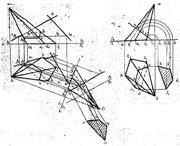
Позиционные задачи Построить линию пересечения поверхностей одним из нижеперечисленных методов: метод секущих плоскостей, концентрических или эксцентрических сфер. Определить видимость поверхностей относительно друг друга и записать их геометрические опеределения. |
 |
Метрические задачи Задача 1. Построить проекции и натуральную величину сечения фигуры заданной плоскостью. Предпочтительно использовать метод перемены одной или двух плоскостей проекций. При решении задачи для нахождения натуральных величин элементов геометрических фигур используют вращение вокруг проецирующей прямой или прямой уровня, замену плоскостей проекций, способ прямоугольного прямоугольника. Задача 2. Построить развертку заданной геометрической фигуры и нанести на ней линию сечения. |